计算机下棋程序设计，以不围棋为例。

作者按：这是数据结构课程的 assignment，本人撰写了本设计报告。

botzone NoGo 棋简单 AI 的设计

小组成员：

• 李秉权 软件学院 2020 级 6 班
• 刘小宝 软件学院 2020 级 6 班
• 刘小明 软件学院 2020 级 6 班
• 王三金 软件学院 2020 级 10 班

1 分工与合作

项目进行的初期，刘小明、王三金与 botzone 对战平台上的机器人进行了多次对弈，结合两人具备的围棋基础，向另外两名队员介绍了不围棋的基本知识和博弈思路，分析了这种游戏与传统围棋的异同。而刘小宝与李秉权两人则进行了文献查找和资料查阅的工作，李秉权总结说，机器博弈的关键在于要有前瞻性^[1]，计算机不仅要能对当前的博弈状态做静态的分析，还要能够预测对手的行动，综合分析比较过后去争取对双方玩家都是折中的游戏状态。刘小宝则大量观看了不围棋的历史对战回放，他提出我们应该侧重对棋局做静态分析，指出我们应该参考模式识别的基本原理来评估棋局局部对双方的厉害关系，并以此为依据构思了几种对已方有利的棋局模式。

项目进行到中期，刘小宝则编码实现了基于棋局局部识别的对弈框架，构思了可选落子位置的静态估值函数的程序接口，并实现了反映必要游戏规则的估值函数作为示例。这为后期队员分头编写功能代码打下了良好的基础。李秉权则对对战平台提供的代码进行了 C++的现代化重构，并整理了常用的程序接口，诸如寻找连通块的气、游戏棋盘的方便输入输出等。此外，李还提出即便我们不了解围棋原理和博弈的基本知识，我们也可以用蒙特卡洛搜索树取得较好的效果，他指出，如果使用他找到的开源搜索树框架我们只需要重写几个关键步骤的实现^[2]，就可以使用这一著名算法进行对局，根据[3]，他认为这一算法可以取得较好的成绩。

项目进行的后期，根据项目中前期的分析研判，我们决定采用刘小宝提出的基于估值函数的博弈算法，因为这种方法相对简单，符合各组员对不围棋游戏的直觉。我们交流讨论之后每个队员分别领取若干估值函数的编写任务，并分头开始编码工作。各队员所承担的编码任务都在四月十五日之前基本完成了。其中，具体的任务记录如下：

队员	完成的编写工作
刘小宝	程序主要逻辑框架、必要的各数据结构、部分估值函数（填眼）
李秉权	部分估值函数（与现有同色棋子连成眼、与现有同色棋子连成线）
刘小明	部分估值函数（填眼、构造平行四边形的第一步、构造平行四边形的第二步）
王三金	部分估值函数（棋局的四角、利于构建居于棋局四角的三角形）

第一阶段的编码工作完成后，由王三金在 botzone 平台上进行了多轮对战，他记录了几种程序常出现的反常行为，并对算法的参数进行了调整，决定从棋局中期开始降低青睐填眼和构造平行四边形的估值函数的权重，刘小明对新的参数进行测试，注意到我们的机器在 20 局之后的构造出的活棋的气的数量由原来的一至三提高到了五至七个。这个过程中李秉权则发现并修正了程序的一处缺陷。

我们认为各成员承担的工作量如下：

成员	百分比
刘小宝	40%
刘小明	20%
李秉权	20%
王三金	20%

由李秉权撰写了本实验报告。

2 参考文献与创新之处

除上面提到的文献外，在项目的前期阶段，我们了解了常见的计算机下棋解决方案，以及围棋基本知识。在编码实现方面，除了老师统一提供的程序示例之外，其他所有代码都是我们队伍分工编写了的，只有部分的思路借鉴了网络上的文献和其他资料。

[1] Search: Games, Minimax, and Alpha-Beta. MIT OpenCourseWare. https://youtu.be/STjW3eH0Cik

[2] C++ MCTS. Konijnendijk. https://github.com/Konijnendijk/cpp-mcts

[3] NoGo Bot. https://fstqwq.pw/nogo-bot/

3 算法思想

概括地说，我们开发过程可以概括为如下两个步骤：

1. 根据实践经验（empirical experience）和领域内知识（domain knowledge），归纳大量的实践观察总结棋局的共性得出操作性强的启示。
2. 将前述专业域内启示，以一个或一组估值函数的形式表达出来，并编码实现，这一过程是我们的工作的主要内容。

具体地说，算法如下：

每次决策都先遍历每一个棋盘上的符合规则的空位，对每个位置都用一批估值函数进行打分，将估值函数的结果累加作为此位置的得分，保留得分最高的空位作为下一步落子的位置。为了方便调试，我们给每一个估值函数都分配了一定的权重，为了进一步提高算法的灵活性，我们还配置了三种不同的权重对应我们划分的对局的前、中、末三个阶段，这样，机器的决策行为可以在对局发展而调整。算法描述如下：

\[\begin{align} 记棋盘位置为P_{xy}(\ x,y\in \{0,1,2,3 ...8\})，记估值函数为F_i(i\in {1,2,3.....n})， \\在棋局回合数a的权重为W_{\omega(a)}^i(a\in\{x|1<=x<=300\}) \\记G_{xy}=\{-1,0,1\}为棋盘上x行y列的状态： \\ G_{xy}=0表示此处没有棋子， G_{xy}=-1表示此处有对手棋子， G_{xy}=1表示此处有己方棋子。 \\ 在回合数a，对P_{i,j}\ where\ G_{i,j}=0，我们记Score_{i,j}=\Sigma^{n}_{f=1}W_{\omega(a)}^fF_f(P_{ij})为这一位置这轮决策的得分， \\最后我们决定在P_{mn}处下棋，s.t. Score_{mn}=max\{Score_{ij}\ where i,j\in\{0,1,2,3 ... 8\}。 \end{align}\]

部分估值函数介绍

估值函数的名字描述的是机器青睐的某种棋局形势，比如：

\[估值函数“能与同色棋子连成线”指的是，\\ 如果在P_{xy}处落子，新落的子能与四方的同色棋子当中一些连成线，则函数值F(P_{xy})>0.\]

填眼

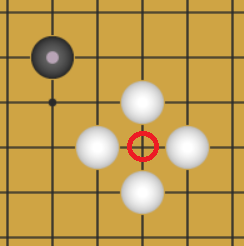
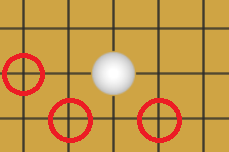
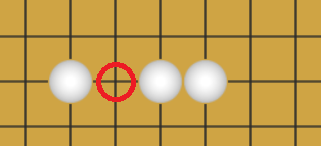
这里的眼指的是四方都是己方棋子的气，这个气已被己方牢牢控制，下在红圈处对局势没有帮助，此估值函数总是输出负数。

青睐有利于构造平行四边形的位置

此套估值函数反映了我们的关键思路之一。刘小明和刘小宝两位同学调研了大量的比赛对局记录，结合他们过去的对围棋的理解，总结说我们应该尽力地在棋盘构造一种由四个棋子在相邻两条棋盘线上构成的图形。二刘认为这种图形能够以最少的棋子控制最多的棋盘气的数量。经反复的试验，在我们的开发框架下，刘小明构思了一套能够选中有利于构造上述图形的新颖的估值函数。

第一步

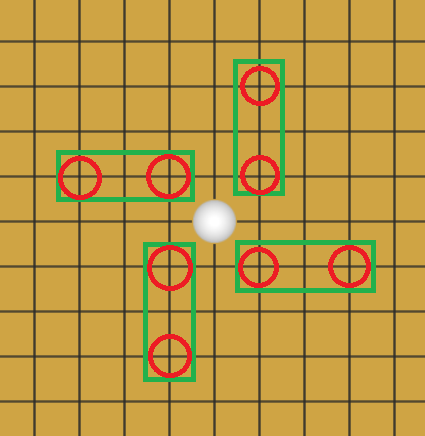
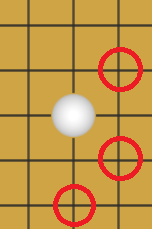
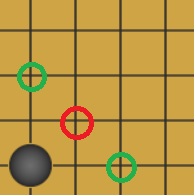
以下图白子所在的位置为例，检查如下四个方向上是否有两个一组的己方棋子存在，某一方向上如果有，就对这个棋子位置增加一个单位的得分。下图四个绿色方框内的两个红旗圈就分别为一组。

第二步

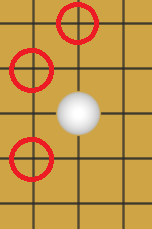
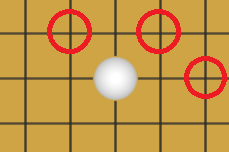
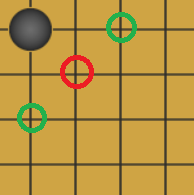
如下图四种情况，如果某一位置周围三个红圈处都存在己方棋子，则给此位置加分，与上一步骤类似，四种情况的得分累加，作为最后的估值函数输出。

优先下在棋局的四角

即对如下位置，估值函数返回正数，其他返回零：

\[P_{8,8},P_{8,0},P_{0,8},P_{0,0}\]

有利于构建棋局四角的三角形

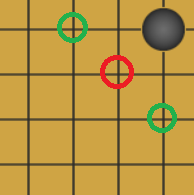
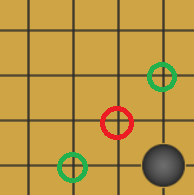
如果我方已有一枚棋子在棋局一角，则对下图红圈位置输出正数，当红圈处已有我方棋子时对绿圈处位置输出正数，其他位置输出零。如下图：

能增加活棋的气的数量

这一指导原则可以转化为如下几个估值函数：

描述	示意图
在此处落子，能构成至少有三个棋子的己方同色连线，如右图红圈处。
在此处落子，能让四方的气之一形成一个眼，如右图红圈处。